专利“接触面温度测量装置”介绍
薛 健
专利号:ZL200620050744.5 专利权人:薛 健
授权公告日期:2007年8月22日 电 话:0731-8876185 13657312654
授权公告号:CN2938049Y 地 址:(410083)长沙中南大学粉末 冶金研究院质检中心
(一)概 述
曾有专家指出,也许除重力等少数性能外,一切物质的性能均与温度有关。此表明温度测量的重要性与普遍性,总的来说,当今温度的测量技术已是十分普遍与成熟,而且伴随着科技的发展仍在不断进步。但对像接触面等某些特殊场合的温度测量,仍是此大家族中的薄弱环节,然而这些场合的测温往往具有特殊意义。本专利至少在以下方面有望得到广泛应用:1、一定的温度对应于一定的物质理化性质及物理与化学反应,人们正是通过这一关系研究及开发新型材料,对于在接触面上的材料,要有效地进行研究就必须测量其表面温度。2、运行的机器由于摩擦或冷却系统及润滑系统故障使局部温度增高。此时不仅浪费能源,更重要的是可能由此造成人身与设备事故,因此几乎无处不在的轴瓦温度测量就显得至关重要,可通过测温监控其运行状态, 3、高效、节能、环保的新型动力机械的开发研究需要知道汽缸内部工作过程中的动态温度变化信息作为有效改进发动机的手段,4、飞机、汽车等刹车盘表面温度影响其摩擦系数等性能,进而影响飞机的安全着陆及汽车的运行,因此表面温度的检测控制是保证其安全的一个有效手段。作为接触面测温的一个应用方面,文献介绍的国内外制动器表面温度测试现行技术主要有:(1)盘面预置热电偶技术(2)盘中预埋热电偶技术(3)制动片中预埋热电偶技术(4)红外线测温技术(5)红外热成像技术(6)制动片表面薄膜热电偶技术(7)制动器表面贴覆易熔合金技术(8)温度记忆螺钉技术等。以上八种测温技术中,1、2、3、6、7、8属接触法测温范畴,4、5属非接触法测温。前者基本上均未实现直接测量接触面温度,均通过测量距离接触面附近某处温度经推算得到接触面温度,误差之大可想而知,而实时测温就更难实现了。而对具有磨损的制动器表面非接触法测温由于看不见接触面这一测温对象更难以得到准确实时测温结果。总之现行测温技术与装置均不能完满解决此领域的温度测量任务。为此,我们在多年研究的基础上,提出了“接触面温度测量装置”专利,克服了传统技术的困难,较为完满地解决了这一长期未能解决的问题。
(二)接触面温度测量装置
专利号为ZL200620050744.5的装置,由特殊温度传感器和测温仪表组成,测温仪表由于其应用环境不同,可以有多种类型,从简单测量最大热电势的毫伏表到可实现实时快速连续测温并具有数据处理功能的计算机检测系统,由于本专利应用的测温仪表与传统应用的类似,这里就不作介绍了。以下着重介绍本专利的核心技术—特殊传感器。
物体1可以是交通工具及各类机器广泛应用的刹车副等材料及装置,物体2则是相应的轴或对偶材料,5和6是由不同材料构成的细热电偶丝,二者相互绝缘并尽量靠近,二热电偶丝用绝缘胶4与物体3固为一体,其端面分别压于接触面上,由于此二热电偶丝端部没有焊在一起,而接触面就起到了传统热电偶焊点的作用,因此其热电势直接反映了热电偶丝与接触面接触处的温度,依照中间导体定律,只要二热电偶丝与接触面接触处的温度相等,则对整个回路的总热电势将不产生影响,其证明如下:
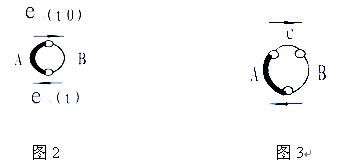
传统热偶丝如图2所示,由热电偶丝a、b组成的热电偶其热电势为
E=eab(t)-eab(t0) ………………………………………(1)
当热电偶丝间加入金属C时,如图3所示,其热电势为
E=eab(t)+ebc(t0)+eca(t0)………………………………....(2)
当(2)式t=t0时,则因各接点温度相等,故总热电势等于零,故有
-eab(t0)=ebc(t0)+eca(t0)…..……………………………..(3)
将(3)式代入(2)式得
E=eab(t)-eab(t0)……………………………………….(4)
式(4)与式(1)全同,由此可得结论如下,
如果二热电偶丝间加入第三导体,只要二热电偶丝与第三导体接点处温度相同,则其热电势与未加之前相等。
该特殊温度传感器的响应速度直接影响到能否实现实时精确测温问题,因此需要做较为详细的讨论。理论可以证明当接触面突然产生一阶跃温升后,热电偶丝输出温度达到接触面最大温升95%所需时间t可由下式求得:
t = ………………………………………(5)
式中:Dt—热电偶丝直径
λt—热电偶丝导热系数
α—接触面材料的热扩散率
λ—接触面材料的导热系数
由上式可见,影响此特殊传感器响应时间有如下诸因素:
1、热电偶丝直径:响应时间与热电偶丝直径的平方成正比,因此为减少实时测温误差应尽量选取细热电偶丝;
2、热电偶丝导热系数:热电偶丝导热系数与响应时间成正比,因此选用导热差的热电偶丝有助于响应时间的减小及响应速度的提高;
3、接触面材料的导热系数与响应时间成反比关系;
4、接触面材料的热扩散率对响应时间亦成反比;
5、进一步研究表明,构成接触面的物体的尺寸、密度与比热等亦与响应时间有关,厚度过小将导致时间增加。
由于传感器各参数的不同,响应时间通常在微秒至毫秒范围内,实测值较上式计算值小,完全可满足工程应用中实时测温的需要。
由此可见,本专利技术的主要优点:1、可直接测得表面温度:在传统热电偶中,直接测得的温度是热电偶焊点的温度,并不是你要测的目标温度,只有当达到完全热平衡时,焊点温度才与目标温度相等。本专利不存在这种假设与转换,因为它直接测得的就是接触面本身的温度;
1、可实现对接触面定点实时测温:由于热电偶很小,通常直径小于1mm,故与接触面的接触点面积也很小,又由于其响应时间通常为毫秒级,因此可实现对接触面的实时、定点、快速测温;
2、适用于任何接触面:在实际应用中经常遇到接触面有相对运动及材料存在磨损情况,由于热电偶丝无焊点,可与材料一同磨损,热电势输出性能不会因磨损而改变;
3、简单易行、经济实用、便于推广:本专利实施中所用热电偶丝、测试仪器仪表热电偶分度以及理论基础等均与传统热电偶测温装置一致,故可充分利用现有软、硬件条件,故能多快好省实现应用及推广。
(三)应用领域
本专利科学实用、市场广阔、简单易行、成本低廉,是具有巨大的经济和社会效益的绿色专利,主要应用领域如下:
1、新型材料研究:机器上的滑动轴承、飞机和汽车的制动器、轮胎等均处于接触面工作状态,以飞机用的摩擦材料为例,为保证飞机的安全,对摩擦材料的机械性能、摩擦系数、工作温度等均有严格要求,而工作温度不仅其本身是一种重要的热物理性能,而且更重要的是由于它能决定材料的理化反应及理化性质,因而是影响材料研究的关键,由此可见,温度是材料研究者的主要耳目,掌握温度及其在不同温度下的材料性能,在温度与其他性能关系的相关理论指导下,就能更快更好的解决材料研究的各种问题,达到多出成果、快出成果、出好成果的目的。
2、新型设备研发:包括新型摩擦试验机、耐磨试验机、地面动力试验台及动力设备的研发。现以地面动力试验台为例加以说明,飞机用摩擦材料在装机试飞前,要经过地面上一系列的严格检验,这种检验要求最大限度模拟飞机实际着陆状态,价值数千万元的地面动力试验台就是为此目的而制造的,此时要求能够测量试验材料表面温度变化的全过程,以实时准确测温为特点的本专利的应用就成了研发新型试验设备的关键,举一反三,对其他类型实验设备及发动机等动力设备亦是如此。
3、安全节能运行的保证:几乎所有机器和交通工具均离不开滑动轴承、汽缸、制动器等部件,以滑动轴承为例,它往往应用于机器和车辆的重负荷部分,在运行中由于摩擦而发热,以汽车为例正常情况下多数温升在100℃左右,如果一旦出现故障,则温度增加,严重时甚至出现抱死而导致重大设备与人身安全事故。因此对这些部分需要准确测温,在正常运行范围内温度的低高反应机械效率的高低,在非常情况下温度的超常升高则是即将发生事故的预警,因此设置测温装置作为车辆、飞机、机器运行监控具有重要意义。同时在研发这些机器设备上也大有用武之地。
4、新型测温仪器的研发:如上所述,如此广泛应用的各种类型接触面测温需要必然导致大量相应测温仪器仪表的研发与生产,由于与该特殊传感器分度与传统热电偶相同以及与之配套仪器仪表基本与传统测温装置相似,因而对其高效、低成本研发、生产与应用极为有利。
(四)应用实例
近几年来,我们对接触面测温技术进行了大量实验研究,在证明其有效性与可行性之后才提出了本专利,作为例证之一,现将摩擦材料研究中对本接触面测温专利的应用作简要介绍。实验是在经过适当改造后的摩擦材料试验机上进行的,该试验机的原有测温方法是在距摩擦静环表面1mm、8mm及15mm处分别装上传统热电偶,测得不同位置的温度后通过计算推出表面温度,为对比方便,我们只加装了专利所介绍的表面测温传感器,其他原有测温装置不变,在对原测温用数据采集及处理系统进行修改补充后,进行了大量实际测试,同时用有限元方法进行了三维温场计算,其结果如图4、图5所示。
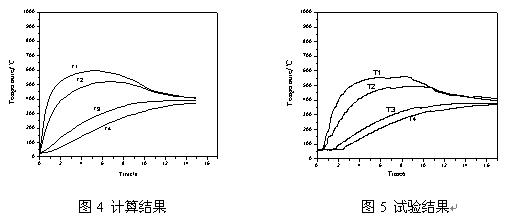
从图5中表面测温曲线T1与传统测温曲线T2、T3、T4对比可以得出以下几点结论:
1、表面温度高于距表面不同距离处的温度,距表面距离愈远则其间温差愈大;
2、表面温度达到其最大值的时间最短、其他各处达到最大值的时间随传感器距表面的增加而增大;
3、各测温曲线间的关系随着试验样品的散热状态的变化而改变;
4、当实验完成,刹车系统松开,接触面脱离接触,使接触面暴露于空气中,则表面温度以超过传统热电偶处的温度下降速度迅速减小。
以上情况进一步证明,表面测温专利技术可实现对接触面准确、实时测温,在快速变化的表面温度下,其测温也存在滞后,但时间是毫秒级的,传统热电偶测温的延时是秒级或更大,换言之,本专利测温速度较传统热电偶高千倍以上。
有限元法三维仿真计算结果如图4所示,该图与图5基本吻合,这也进一步证明实验结果与理论的一致性。
致谢:作者对王辉、雷宝灵在实验及计算方面所做的大量工作表示感谢! |
